Vitesse de la lumière

En bref: On a cru pendant longtemps que la lumière se propageait de manière instantanée. Nous savons aujourd'hui que ce n'est pas le cas, et la vitesse de la lumière vaut 299 792 458 mètres par seconde, ce qui vaut environ un milliard de kilomètres par heure. Cette valeur a été fixée lors de la 15e Conférence Générale des poids et mesures, en 1975. Entre les premières intuitions d'Alhazen, mathématicien perse du moyen-âge, et la définition de la vitesse de la lumière comme une constante universelle, de nombreuses mesures ont été effectuées, avec des méthodes de plus en plus précises. Galilée, au 17e siècle, a tenté pour la première fois de prouver que la vitesse de la lumière était finie. Mais cette vitesse est tellement élevée que ses expériences ne seront pas concluantes. Peu après, Cassini et Roemer vont observer les éclipses de Io, un satellite de Jupiter. Ils vont effectuer des prédictions sur les horaires des éclipses, mais vont se rendre compte que les éclipses ont parfois du retard, parfois de l'avance. Roemer explique ces retards par le fait que la lumière a une vitesse finie, et qu'elle ne met donc pas le même temps pour atteindre la Terre l'éloignement de la Terre par rapport à Jupiter. Au 19e siècle, Fizeau réalise son expérience de la roue dentée entre Suresnes et Montmartre. Il surestime alors la vitesse de la lumière. Léon Foucault va effectuer une expérience similaire à l'aide de miroirs tournant, en laboratoire. Dès la fin du 19e siècle, la communauté scientifique admet que la lumière se comporte comme une onde. En 1905, Einstein publie sa théorie de la relativité restreinte, qui énonce en particulier le fait que la vitesse de la lumière dans le vide est constante et ne dépend ni du mouvement de la source lumineuse ni de l'observateur. Il est alors possible de déterminer cette vitesse, que l'on va maintenant nommer célérité, avec de plus en plus de précision, jusqu'en 1983 où elle a été fixée à 299 792 458 m/s.

Galilée, les collines et les lanternes

C’est Alhazen, un mathématicien perse du moyen-âge, qui a eu en premier l’intuition que la vitesse de la lumière était finie, même s’il n’a rien pu prouver. Au 17e siècle, Galilée a la même intuition, et il pense que si on ne peut pas s’en rendre compte à l’oeil nu, c’est parce que la lumière se propage très rapidement. Il va chercher à mesurer cette vitesse de propagation.

Son expérience est simple: deux observateurs se placent chacun au sommet d’une colline, les deux collines étant séparées d’environ 1800m. Ils ont chacun une lanterne, masquée au départ. Le premier observateur possède aussi une clepsydre, un instrument à eau qui fonctionne sur le même principe qu’un sablier et qui permet de mesurer le temps. Il va démasquer sa lanterne et déclencher la clepsydre au même moment. Le deuxième observateur va démasquer sa lanterne dès qu’il aperçoit la lumière de la première lanterne. Au moment où le premier observateur voit la lanterne de son compagnon, il arrête la clepsydre. Avant tout cela, les deux observateurs, proches l'un de l'autre, vont s'entrainer à démasquer leur lanterne le plus rapidement possible dès qu'ils voient la lueur de l'autre lanterne. Ainsi ils réduisent leur temps de réaction et peuvent le mesurer. Ils étalonnent en quelque sorte leurs mesures.

En théorie, cette expérience donne le temps que met la lumière pour parcourir environ 3600m. En pratique, la lumière semble instantanée. Ceci est dû au fait que la distance qui sépare les deux hommes est trop faible, la lumière met seulement quelques millionièmes de secondes pour faire l’aller-retour entre les deux hommes.

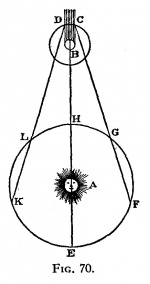
La vitesse d'un objet s'exprime par la relation [math]\displaystyle{ v=\frac{d}{t} }[/math] avec [math]\displaystyle{ v }[/math] la vitesse, [math]\displaystyle{ d }[/math] la distance parcourue et [math]\displaystyle{ t }[/math] le temps mis par l'objet pour parcourir cette distance. Dans le système international d'unités (SI), la vitesse s'exprime en m/s. Dans la vie de tous les jours, on utilise le plus souvent des km/h (par exemple pour exprimer la vitesse d'une voiture). Pour convertir des m/s en km/h, il suffit de multiplier par 3,6 et pour convertir des km/h en m/s, il faut diviser par 3,6. Par exemple, une voiture qui roule à 90km/h roule à 25m/s.

Observation des éclipses de Io

Toujours au 17e siècle, Jean-Dominique Cassini observe les éclipses de Io, un des satellites naturels de Jupiter. Il va utiliser les lois de Kepler, qui décrivent la mécanique céleste, pour effectuer des prévisions sur les horaires auxquels ces éclipses ont lieu. Mais il se rend compte que ses observations ne collent pas à ses prévisions: à certains moments de l'année, les éclipses ont du retard, à d'autres, elles ont de l'avance.

Ole Römer, un astronome danois qui travaille avec Cassini, explique ce phénomène par le fait que la distance entre la Terre et Jupiter n'est pas toujours la même. En effet, si on regarde l'image ci-contre, la Terre est plus éloignée de Jupiter lorsqu'elle se trouve au point F que lorsqu'elle se trouve au point G. Le point B représente Jupiter, les points C et D représentent les positions où Io disparait et apparait derrière Jupiter tandis que les points E, F, G, H, L et K représentent les différentes positions de la Terre autour du Soleil. Si la lumière a une vitesse finie, alors elle met plus de temps pour parcourir une distance plus grande, ce qui explique le retard des éclipses. James Bradley, un astronome anglais, va réussir à prouver cette hypothèse une cinquantaine d'années plus tard grâce à l'aberration de la lumière et va estimer la vitesse de la lumière autour de 300 000km/s.

Aberration de la lumière: Imaginons que nous sommes en voiture, qu'il pleut, et qu'il n'y a pas de vent. Si nous sommes à l'arrêt, la pluie semble venir d'au-dessus de nos têtes (et c'est effectivement le cas). Mais si nous roulons à une certaine vitesse, la pluie semble venir de devant nous. Il se produit le même phénomène avec la lumière des étoiles, puisque la Terre tourne autour du Soleil et a donc une vitesse non nulle par rapport aux étoiles. James Bradley a découvert ce phénomène en 1725, apportant ainsi une preuve que la Terre tourne autour du Soleil.

(Question: Comment connait-on la distance qui sépare la Terre de Jupiter à cette époque?)

Roue dentée de Fizeau

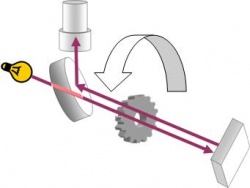
Au milieu du 19e siècle, il est admis par la communauté scientifique que la lumière a une vitesse finie. En 1849, Hippolyte Fizeau s'inspire de Galilée et améliore son dispositif. Il effectue ses mesures entre son balcon, à Suresnes, et la butte Montmartre, à exactement 8633m de distance.

Une source de lumière est placée à Suresnes. Le rayon lumineux va passer à travers un miroir semi-réfléchissant, puis à travers une roue dentée. Il va ensuite continuer jusqu'à un miroir réfléchissent, à Montmartre, où il va être renvoyé vers Suresnes, en passant à nouveau par la roue dentée. Là, l'observateur va pouvoir l'observer.

Si la roue dentée est au repos, le rayon lumineux va passer à travers un creux entre de dents à l'aller, et par le même creux au retour. Mais dès qu'un moteur fait tourner la roue, le rayon passe à travers un creux à l'aller, mais se retrouve bloqué par une dent au retour. C'est seulement à partir d'une certaine vitesse de rotation de la roue que le rayon va pouvoir passer par le creux suivant au retour. En mesurant cette vitesse de rotation, on peut déterminer le temps qu'a mis le rayon lumineux pour effectuer l'aller-retour entre la roue et le miroir, et donc on peut calculer la vitesse de la lumière.

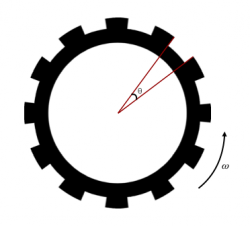
Explication plus détaillée:

On note:

[math]\displaystyle{ d }[/math] la distance qui sépare la roue dentée du miroir réfléchissant,
[math]\displaystyle{ t }[/math] le temps mis par la lumière pour parcourir deux fois la distance [math]\displaystyle{ d }[/math] (pour l'aller-retour),
[math]\displaystyle{ \theta }[/math] l'angle représenté par une dent ou un creux, exprimé en degrés (voir dessin ci-contre),
[math]\displaystyle{ \omega }[/math] la vitesse de rotation de la roue dentée, que l'on exprimera ici en degré par seconde.

On note [math]\displaystyle{ c }[/math] la vitesse de la lumière.

On sait que [math]\displaystyle{ c=\frac{2d}{t} }[/math]. On peut également dire que [math]\displaystyle{ t=\frac{\theta }{\omega } }[/math]: on a en effet degrés sur des degrés par seconde, ce qui nous donne bien des secondes.

On peut donc écrire: [math]\displaystyle{ c=\frac{2d\omega }{\theta } }[/math].

La roue dentée possède 720 dents et 720 creux de tailles égales. Une dent (ou un creux) couvre donc un angle de 0,25°. Fizeau a mesuré une vitesse de rotation d'environ 12,6 tours par seconde pour que la lumière passe à l'aller par un creux et au retour par le creux suivant, ce qui équivaut à environ 4536 degrés par seconde. La distance [math]\displaystyle{ d }[/math] vaut 8633m. Avec ces paramètres, on obtient une valeur de [math]\displaystyle{ c }[/math] autour de 313 000km/s. (incertitude?)

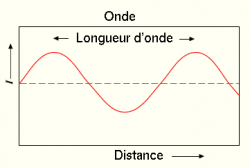
Fréquence et longueur d'onde

A la fin du 19e siècle, il est admis que la lumière se comporte comme une onde. Or, une onde est définie par deux caractéristiques: sa longueur d'onde, et sa fréquence.

Représentons une onde comme une vague. La longueur d'onde, notée [math]\displaystyle{ \lambda }[/math], est la distance qui sépare deux crêtes de cette vague. La fréquence, notée [math]\displaystyle{ \nu }[/math] (prononcer "nu"), est, si on se place en un point donné, le nombre de crêtes qui passent par ce point pendant une seconde. Elle s'exprime en Hertz (Hz). On appelle [math]\displaystyle{ T }[/math] la période de la vague, c'est à dire, en un point fixe, le temps entre deux crêtes successives. La fréquence est alors l'inverse de la période. On a [math]\displaystyle{ f=\frac{1}{T} }[/math].

On peut maintenant écrire que la vitesse d'une onde, appelée célérité, est égale à sa fréquence multipliée par sa longueur d'onde. Soit: [math]\displaystyle{ c=\lambda\times f }[/math]. Mais comment mesure-t-on la fréquence et la longueur d'onde de la lumière? (Vous le saurez bientôt!)

On découvre également à cette époque que la lumière n'est qu'une infime partie du spectre électromagnétique. Il existe donc une multitude d'ondes électromagnétiques avec des longueurs d'ondes et des fréquences variées, mais qui se déplacent toutes à la vitesse de la lumière!

Une constante universelle

Après la seconde guerre mondiale, les ondes électromagnétiques sont de plus en plus utilisées pour communiquer et sont donc de mieux en mieux comprises. Les mesures de la vitesse de la lumière sont alors de plus en plus précises. Mais l'étalon du mètre, en platine iridié, est imprécis face à ces mesures. Or, la vitesse s'exprime en mètres par seconde. Elle dépend donc de la définition du mètre. Il a alors été décidé, en 1983, de fixer la vitesse de la lumière comme constante et de faire dépendre la définition du mètre de cette constante. Ainsi, le mètre ne dépend plus que de la seconde.

Nous avons trois unités, qui sont liées entre elles: le mètre, la seconde et la vitesse de la lumière. Il suffit d'en fixer deux, pour connaitre la troisième. Il a été décidé de fixer la seconde et la vitesse de la lumière.

La vitesse de la lumière dans le vide est donc: [math]\displaystyle{ c }[/math]=299 792 458 m/s.

Pour en savoir plus

De nombreuses autres méthodes ont été utilisées au fil des siècles pour déterminer la vitesse de la lumière. Voici quelques vidéos à propos des méthodes dont nous avons déjà parlé, mais aussi à propos des autres méthodes:

Les magiciens de la lumière: un docu-fiction produit par le Service de Création AudioVisuelle de la Faculté des Sciences d'Orsay (61min)

Comment ont-ils su que la lumière avait une vitesse? Témoignage de Pierre Lauginie (7min)

L'histoire des mesures de la vitesse de la lumière racontée par Jamy (54min)