« Distances sur Terre » : différence entre les versions
m (justification du texte) |
|||
| Ligne 3 : | Ligne 3 : | ||
{{En bref| Explication des différentes méthodes qui existent pour mesurer des distances sur Terre. (Work in Progress) }} | {{En bref| Explication des différentes méthodes qui existent pour mesurer des distances sur Terre. (Work in Progress) }} | ||
== La triangulation == | == La triangulation == | ||
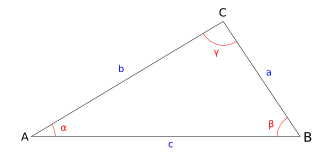
[[File:triangle.png|frame]] La triangulation est une technique inventée au 17e siècle qui permet de calculer des longueurs à partir de mesures d'angles. Elle a notamment été utilisée à la fin du 18e siècle par [[#Le méridien de Méchain et Delambre|Méchain et Delambre]], lors de la définition du [[mètre]]. Cette méthode fait appel à la trigonométrie et se base sur la loi des sinus:<math> \frac{a}{sin\alpha }=\frac{b}{sin\beta }=\frac{c}{sin\gamma }</math>. Elle part du principe que si on connait deux angles et un côté d'un triangle, alors on en connait tous les côtés. On peut ainsi mesurer de longues distances plus précisément et plus facilement qu'en mettant des règles de longueur connues bout à bout. | [[File:triangle.png|frame]] La triangulation est une technique inventée au 17e siècle qui permet de calculer des longueurs à partir de mesures d'angles. Elle a notamment été utilisée à la fin du 18e siècle par [[Mètre#Le méridien de Méchain et Delambre|Méchain et Delambre]], lors de la définition du [[mètre]]. Cette méthode fait appel à la trigonométrie et se base sur la loi des sinus:<math> \frac{a}{sin\alpha }=\frac{b}{sin\beta }=\frac{c}{sin\gamma }</math>. Elle part du principe que si on connait deux angles et un côté d'un triangle, alors on en connait tous les côtés. On peut ainsi mesurer de longues distances plus précisément et plus facilement qu'en mettant des règles de longueur connues bout à bout. | ||
Version du 9 juin 2016 à 10:13
|
|
La triangulation
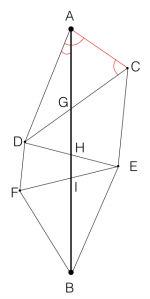
Le principe est relativement simple: il faut tracer des triangles donc les sommets sont visibles les uns depuis les autres (comme des clochers, des collines...) et y placer un signal. La seule mesure qui n'est pas un angle est celle d'un côté du triangle, au départ. Toutes les autres mesures nécessaires sont des mesures d'angles, effectuées grâce au cercle répétiteur.
Prenons un exemple concret:
On cherche à mesurer la distance AB, représentée sur le schéma. On peut décomposer cette distance ainsi: [math]\displaystyle{ AB=AG+GH+HI+IB }[/math]. Le côté en rouge représente la base du premier triangle, que l'on a mesurée.
- On travaille tout d'abord dans le triangle ACD. On connait AC, ainsi que les angles [math]\displaystyle{ \widehat{DAC} }[/math] et [math]\displaystyle{ \widehat{ACD} }[/math]. On peut donc calculer [math]\displaystyle{ \widehat{ADC} }[/math], car on sait que dans un triangle, la somme des angles vaut 180°. Grace à la loi des sinus, on peut calculer les côtés AD et DC. Nous avons donc résolu le triangle ACD.
- Plaçons nous maintenant dans le triangle AGD: on peut mesurer l'angle [math]\displaystyle{ \widehat{ADG} }[/math] (que l'on connait en fait déjà, puisqu'il s'agit de l'angle [math]\displaystyle{ \widehat{ADC} }[/math]) , ainsi que l'angle [math]\displaystyle{ \widehat{DAG} }[/math], qui est l'angle entre le côté AD et le méridien, que l'on appelle azimut. Nous connaissons également le côté AD. A nouveau, nous avons un triangle dont on connait un côté ainsi que deux angles. On peut donc calculer les côtés DG et AG. Nous avons une première partie de notre distance AB!
- On répète ces mesures et ces calculs dans le triangle ACG, afin de connaitre la distance CG. Ainsi on connait le côté DC, qui est égal à [math]\displaystyle{ DG+CG }[/math].
- Et ainsi de suite, on travaille dans le triangle DCE, et de triangle en triangle on finit par connaitre chacun des morceaux de notre distance AB!
Pour chaque triangle, il suffit donc d'effectuer des mesures d'angles depuis deux signaux sur trois, ce qui rend la tache relativement aisée: imaginez un triangle dont les sommets sont deux collines et un clocher. Il n'est pas nécessaire d'effectuer des mesures depuis le haut du clocher, ce qui facilite grandement les choses !
Il faut toutefois ajouter qu'en pratique, les sommets des triangles, donc les signaux, ne sont pas tous à la même hauteur. Il faut alors mesurer aussi l'angle entre le côté du triangle et la verticale. De plus, la Terre est ronde donc les côtés des triangles sont courbes, ce qui complique encore les calculs.
Le cercle répétiteur

Cet instrument, mis au point par Jean-Charles de Borda et amélioré par Etienne Lenoir, permet de mesurer les angles avec une grande précision. Il permet en effet de réaliser plusieurs mesures du même angle, sans remettre l'instrument au zéro, ce qui réduit considérablement l'incertitude sur la mesure.
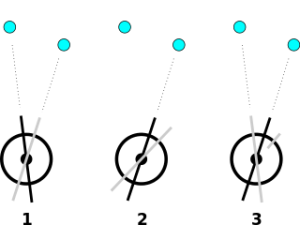
L'instrument est un cercle où sont gradués les angles. Deux lunettes sont situés sur ce cercle. Il faut tout d'abord viser les signaux avec les lunettes: une lunette sur chaque signal (1). On verrouille cette position, et on fait pivoter le système pour que la lunette de gauche vise le signal de droite (2). On note alors la position de la lunette de droite, et on recommence la mesure en visant à nouveau le signal de gauche (3). On peut ainsi effectuer un grand nombre de mesures rapidement.
