Distances sur Terre

En bref: Pour mesurer la distance entre deux points, la première chose à laquelle on pense est utiliser une règle, ou un mètre ruban. Mais pour de grandes distances, comme par exemple la distance qui sépare deux villes, cette technique n'est pas la plus pratique. Il faudrait utiliser un mètre-ruban très long, ou bien mettre plusieurs règles bout à bout. La technique de triangulation permet de mesurer de grandes distances plus facilement, à partir de mesures d'angles. Pour les distances plus petites, comme l'écart entre deux murs ou la largeur d'une rue, il existe aujourd'hui des appareils électroniques qui peuvent prendre ces mesures à distance.

La triangulation

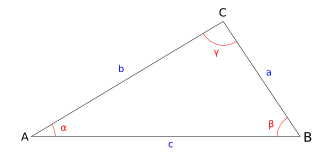
La triangulation est une technique inventée au 17e siècle qui permet de calculer des longueurs à partir de mesures d'angles. Elle a notamment été utilisée à la fin du 18e siècle par Méchain et Delambre, lors de la définition du mètre. Cette méthode fait appel à la trigonométrie et se base sur la loi des sinus:[math]\displaystyle{ \frac{a}{sin\alpha }=\frac{b}{sin\beta }=\frac{c}{sin\gamma } }[/math]. Elle part du principe que si on connait deux angles et un côté d'un triangle, alors on en connait tous les côtés. On peut ainsi mesurer de longues distances plus précisément et plus facilement qu'en mettant des règles de longueur connues bout à bout.

Le principe est relativement simple: il faut tracer des triangles donc les sommets sont visibles les uns depuis les autres (comme des clochers, des collines...) et y placer un signal. La seule mesure qui n'est pas un angle est celle d'un côté du triangle, au départ. Toutes les autres mesures nécessaires sont des mesures d'angles, effectuées grâce au cercle répétiteur.

Prenons un exemple concret:

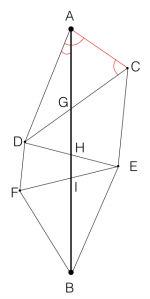
On cherche à mesurer la distance AB, représentée sur le schéma. On peut décomposer cette distance ainsi: [math]\displaystyle{ AB=AG+GH+HI+IB }[/math]. Le côté en rouge représente la base du premier triangle, que l'on a mesurée.

On travaille tout d'abord dans le triangle ACD. On connait AC, ainsi que les angles [math]\displaystyle{ \widehat{DAC} }[/math] et [math]\displaystyle{ \widehat{ACD} }[/math]. On peut donc calculer [math]\displaystyle{ \widehat{ADC} }[/math], car on sait que dans un triangle, la somme des angles vaut 180°. Grace à la loi des sinus, on peut calculer les côtés AD et DC. Nous avons donc résolu le triangle ACD.
Plaçons nous maintenant dans le triangle AGD: on peut mesurer l'angle [math]\displaystyle{ \widehat{ADG} }[/math] (que l'on connait en fait déjà, puisqu'il s'agit de l'angle [math]\displaystyle{ \widehat{ADC} }[/math]) , ainsi que l'angle [math]\displaystyle{ \widehat{DAG} }[/math], qui est l'angle entre le côté AD et le méridien, que l'on appelle azimut. Nous connaissons également le côté AD. A nouveau, nous avons un triangle dont on connait un côté ainsi que deux angles. On peut donc calculer les côtés DG et AG. Nous avons une première partie de notre distance AB!
On répète ces mesures et ces calculs dans le triangle ACG, afin de connaitre la distance CG. Ainsi on connait le côté DC, qui est égal à [math]\displaystyle{ DG+CG }[/math].
Et ainsi de suite, on travaille dans le triangle DCE, et de triangle en triangle on finit par connaitre chacun des morceaux de notre distance AB!

Pour chaque triangle, il suffit donc d'effectuer des mesures d'angles depuis deux signaux sur trois, ce qui rend la tache relativement aisée: imaginez un triangle dont les sommets sont deux collines et un clocher. Il n'est pas nécessaire d'effectuer des mesures depuis le haut du clocher, ce qui facilite grandement les choses !

Il faut toutefois ajouter qu'en pratique, les sommets des triangles, donc les signaux, ne sont pas tous à la même hauteur. Il faut alors mesurer aussi l'angle entre le côté du triangle et la verticale. De plus, la Terre est ronde donc les côtés des triangles sont courbes, ce qui complique encore les calculs.

Le cercle répétiteur

Cet instrument, mis au point par Jean-Charles de Borda et amélioré par Etienne Lenoir, permet de mesurer les angles avec une grande précision. Il permet en effet de réaliser plusieurs mesures du même angle, sans remettre l'instrument au zéro, ce qui réduit considérablement l'incertitude sur la mesure.

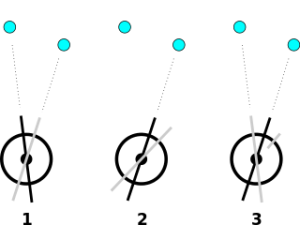
L'instrument est un cercle où sont gradués les angles. Deux lunettes sont situés sur ce cercle. Il faut tout d'abord viser les signaux avec les lunettes: une lunette sur chaque signal (1). On verrouille cette position, et on fait pivoter le système pour que la lunette de gauche vise le signal de droite (2). On note alors la position de la lunette de droite, et on recommence la mesure en visant à nouveau le signal de gauche (3). On peut ainsi effectuer un grand nombre de mesures rapidement.

Télémétrie laser

Il existe aujourd'hui des appareils qui permettent de mesurer des distances sans contact. Toutefois ils ne fonctionnent que pour des distances allant jusqu'à quelques centaines de mètres.

On peut ainsi mesurer la distance entre le télémètre et un mur, par exemple. Le principe est le suivant:

Un signal est envoyé en ligne droite par le télémètre vers le mur. Il va alors se réfléchir contre ce mur, et va revenir vers le télémètre qui va le détecter. Il suffit alors de mesurer le temps mis par le signal pour effectuer l'aller-retour, sachant qu'il se déplace à la vitesse de la lumière.

La distance [math]\displaystyle{ D }[/math] entre le télémètre et le mur vaut alors: [math]\displaystyle{ D=\frac{1}{2}c\Delta t }[/math] avec [math]\displaystyle{ c }[/math] la vitesse de la lumière et [math]\displaystyle{ \Delta t }[/math] le temps entre l'émission et la réception du signal.

Le même principe est employé par les chauve-souris pour se repérer grâce à l'écholocalisation. La différence est qu'elles émettent des ultrasons, qui sont des ondes sonores, alors que la télémétrie laser utilise des ondes électromagnétiques.

Géodésie spatiale

Pour mesurer de plus grandes distances, des satellites artificiels peuvent être utilisés.

Pour plus de détails, voir le paragraphe suivant: Géodésie spatiale

Bibliographie/Webographie

BOUTELOUP, Didier. Topométrie: Mesure des distances. [en ligne]. IGN/ENSG. [consulté le 4 juillet 2016]. Disponible sur internet: <http://www.univ-valenciennes.fr/coursenligne/topographie/partie3/papier.pdf>

OBSPM: « c » à Paris, Vitesse de la lumière : histoires et expériences [en ligne] Exposition de l'Observatoire de Paris et de l'Université Paris VI - Pierre et Marie Curie réalisée en 2005. [consulté le 4 juillet 2016]. Disponible sur internet: <http://expositions.obspm.fr/lumiere2005/triangulation_plus.htmll>