Mètre

Origine du mètre

Avant le 18e siècle, pour mesurer les longueurs, différentes unités coexistent, qui peuvent varier selon les régions ou la taille de l'objet mesuré: le pied, par exemple, le pouce, ou encore la lieue, qui est à l'origine la distance que peut parcourir un homme en une heure. Ces grandeurs varient selon les personnes et ne sont donc pas universelles.

En 1790, aux Etats-Unis, le président Thomas Jefferson propose un système décimal d'unités pour simplifier les transactions et limiter les fraudes, mais le Congrès américain oublie vite l'idée. C'est en France, dans le climat propice aux innovations qu'est la révolution française, que l'uniformisation des unités a été décidée.

En 1791, une commission chargée de fixer la base de l'unité des mesures "à tous les temps, à tous les peuples" est créée. Cette commission cherche alors à rapporter ces unités à un étalon universel qui servirait de référence et serait basé sur un phénomène naturel, et non pas sur la longueur du pouce du roi. Plusieurs propositions sont alors faites: la longueur du pendule battant la seconde, ou la dix millionième partie du quart du méridien terrestre.

Le pendule battant la seconde

Schéma d'un pendule simple

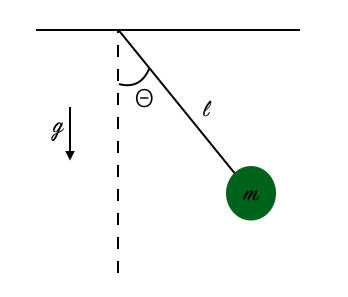
Un pendule simple est une masse ponctuelle, c'est à dire en pratique de faible dimension, accrochée à un fil de masse négligeable. Sa position d'équilibre est la position verticale. Si on écarte le pendule de cette position d'équilibre, il va osciller périodiquement en décrivant un arc de cercle sous l'effet de la pesanteur. On peut montrer que la période des oscillations s'exprime par la relation: .

La période d'un pendule est le temps que met la masse pour effectuer un aller-retour en partant d'une position donnée.

Jean Picard, un astronome français du 17e siècle, propose de prendre comme étalon universel la longueur d'un pendule simple qui bat la seconde. Il entend par là un pendule dont la demi-période vaut une seconde.

La période du pendule dépend de g, l'accélération de la pesanteur. Or, cette accélération n'est pas constante sur Terre: elle dépend de plusieurs paramètres, dont la latitude et l'altitude. L'étalon n'est donc pas universel, il dépend de l'endroit où on se trouve. C'est principalement pour cette raison que le quart de méridien a été choisi comme référence à la place du pendule.

Le méridien de Méchain et Delambre

Un peu d'histoire...

• 1971: le quart de méridien terrestre est choisi comme unité de longueur. Un mètre représente alors la dix millionième partie de ce quart de méridien.

A cette époque, on appelle méridien terrestre un cercle complet autour de la Terre passant par ses deux pôles.

Les astronomes Pierre Méchain et Jean-Baptiste Delambre sont alors chargés de mesurer la distance entre Dunkerque et Barcelone.

Pierre Méchain (Stoyan R. et al. Atlas of the Messier Objects: Highlights of the Deep Sky. — Cambridge: Cambridge University Press, 2008. — P. 23.)

Jean-Baptiste Delambre (Henri Coroênne — Bibliothèque de l’Observatoire de Paris)

Méchain part de Barcelone tandis que Delambre part de Dunkerque, les deux astronomes doivent se retrouver à Rodez. Ils vont utiliser la méthode de triangulation.

Méridienne de Paris (D'après travaux de J. Cassini - BnF, Gallica) Cercle répétiteur de Borda (François Arago - Extrait de "Astronomie populaire" Tome 3 de François ARAGO sur Wikisource) Cette méthode avait déjà été utilisée par Cassini au début du 18e siècle pour déterminer la longueur de la méridienne de Paris. Toutefois les mesures effectuées par Méchain et Delambre seront beaucoup plus précises grâce au perfectionnement cercle répétiteur, mis au point par Borda et amélioré par Lenoir. Cet instrument permet de mesurer des angles avec une grande précision en répétant les mesures de nombreuses fois.

Le contexte historique et politique de l'époque va fortement ralentir les mesures. Le périple, qui devait durer un an, en durera 7. Delambre souhaite effectuer ses mesures depuis les stations utilisées par Cassini. Mais la plupart on été détruites, ou nécessitent d'importants travaux de rénovation. De plus, sa progression est ralentie car le peuple est majoritairement anti-royaliste, et son laissez-passer est signé directement par Louis XVI. La prison le guette. Il réussit tout de même à terminer les mesures de quatorze stations en 8 mois. Il est alors à Paris et obtient un nouveau passeport, cette fois-ci non signée par le roi, qui a été guillotiné le 21 janvier 1793.

• Mars 1793: La France déclare la guerre à l'Angleterre et à l'Espagne. Méchain termine toutefois ses mesures juste avant la déclaration de guerre, mais il est contraint de résider à Barcelone. Il se rend alors chez un ami, où il est victime d'un grave accident qui le plonge dans le coma. Il en sort une semaine plus tard, avec les côtes et l'épaule droite cassées.

• 1er août 1793: A Paris, un mètre provisoire est défini. Seize mètres étalons sont disposés à Paris, dans les lieux les plus fréquentés. Aujourd'hui il en reste deux: un au 36 rue de Vaugirard, et un autre au 13 de la place Vendôme.

  

  Mètre étalon, au 36 rue de Vaugirard (LPLT/Wikimedia commons)

• Décembre 1793: Delambre est destitué de la Commission des poids et mesures pour avoir soutenu Lavoisier, considéré comme traitre de la nation. La France est alors en pleine période de Terreur. Les opérations de mesures de la Méridienne sont interrompues pendant dix-sept mois. Méchain se réfugie en Italie pendant un an.

• 1795: Une loi institue le système métrique décimal: Art. 2: Il n'y aura qu'un seul étalon des poids et mesures pour toute la France ; ce sera une règle de platine sur laquelle sera tracé le mètre, qui a été adopté pour l'unité fondamentale de tout le système des mesures. Les mesures seront marquées du poinçon de la République. Une Agence temporaire des poids et mesures est créée pour remplacer l'ancienne Commission. Delambre et Méchain sont appelés à reprendre leurs mesures. Méchain s'occupe alors de relier les triangles de la frontière entre la France et l'Espagne, la guerre étant finie. Cela lui prend trois mois, malgré les conditions météorologiques et géographiques difficiles.
• 1796: L'Agence temporaire est remplacée par le Bureau des poids et mesures.
• 1798: Delambre et Méchain ont fini tous les triangles, et se retrouvent à Carcassonne après plus de six ans de séparation. Il se rendent ensemble à Paris à la fin du mois de novembre, où le mètre "vrai et définitif" est défini. Il s'avère alors qu'il est plus court que le mètre temporaire, mais la différence est négligeable pour les usages courants. Les mètres provisoires déjà diffusés vont être conservés et vont devenir définitifs. Aujourd'hui, il s'avère que le mètre temporaire est plus proche du mètre actuel que le mètre "vrai"!

La triangulation

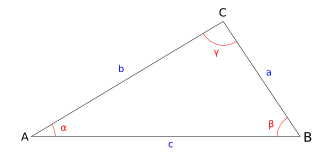
La triangulation est une technique inventée au 17e siècle qui permet de calculer des longueurs à partir de mesures d'angles. Cette méthode fait appel à la trigonométrie et se base sur la loi des sinus: . Elle part du principe que si on connait deux angles et un côté d'un triangle, alors on en connait tous les côtés. On peut ainsi mesurer de longues distances plus précisément et plus facilement qu'en mettant des règles de longueur connues bout à bout.

Le principe est relativement simple: il faut tracer des triangles donc les sommets sont visibles les uns depuis les autres (comme des clochers, des collines...) et y placer un signal. La seule mesure qui n'est pas un angle est celle d'un côté du triangle, au départ. Toutes les autres mesures nécessaires sont des mesures d'angles, effectuées grâce au cercle répétiteur.

Prenons un exemple concret:

Schéma de triangulation

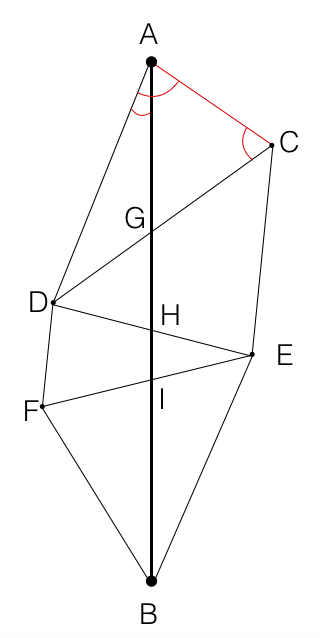
On cherche à mesurer la distance AB, représentée sur le schéma. On peut décomposer cette distance ainsi: AB=AG+GH+HI+IB. Le côté en rouge représente la base du premier triangle, que l'on a mesurée.

• On travaille tout d'abord dans le triangle ACD. On connait AC, ainsi que les angles DAC et ACD. On peut donc calculer ADC, car on sait que dans un triangle, la somme des angles vaut 180°. Grace à la loi des sinus, on peut calculer les côtés AD et DC. Nous avons donc résolu le triangle ACD.
• Plaçons nous maintenant dans le triangle AGD: on peut mesurer l'angle ADG, ainsi que l'angle DAG, qui est l'angle entre le côté AD et le méridien, que l'on appelle azimut. Nous connaissons également le côté AD. A nouveau, nous avons un triangle donc on connait un côté ainsi que deux angles. On peut donc calculer les côtés DG et AG. Nous avons une première partie de notre distance AB!
• On répète ces mesures et ces calculs dans le triangle ACD, afin de connaitre la distance CG. Ainsi on connait le côté DC, qui est égal à DG+CG.
• Et ainsi de suite, on travaille dans le triangle DCE, et de triangle en triangle on finit par connaitre chacun des morceaux de notre distance AB!

Il faut également ajouter qu'en pratique, les sommets des triangles, donc les signaux, ne sont pas tous à la même hauteur. Il faut alors mesurer aussi l'angle entre le côté du triangle et la verticale. De plus, la Terre est ronde donc les côtés des triangles sont courbes, ce qui complique encore les calculs.