Grandeur, valeur et unité
La mesure est un aspect primordial des sciences car elle permet de caractériser les objets et phénomènes que l’on observe, et d’en discuter précisément entre physiciens. Pour comprendre l’intérêt d’avoir un système international qui décrit la façon dont on exprime la mesure, il faut d’abord comprendre des notions très importantes dans ce domaine : la grandeur et l’unité.
Grandeur, valeur et unité
Pour comprendre la différence entre grandeur et unité je vous propose de prendre un exemple très concret de mesure.
Imaginez que vous possédez un bâton et que vous souhaitez indiquer sa longueur à un de vos amis.
Vous remarquez que votre ami possède le même capuchon de stylo que vous, ainsi il constituera la référence pour votre mesure.
Vous allez reporter la taille du capuchon le long du bâton afin de le mesurer.
- Dans cet exemple, la grandeur mesurée correspond à la longueur du bâton , tandis que le capuchon correspond à l’unité, et le résultat 5 capuchons correspond à la valeur de la longueur du bâton. L’unité est donc une grandeur de référence, qui permet de transmettre une information commune à tous, la longueur.
Il faut remarquer que l’unité, la longueur de référence est un choix !!! On aurait très bien pu décider de mesurer le bâton en unité de stylo bille.
De façon équivalente, la longueur du bâton peut également s’exprimer comme :
Quelle que soit l’unité de référence que l’on choisit, la vraie longueur du bâton, elle, reste inchangée. Le bâton est le même dans les 2 cas, mais la valeur de sa mesure est différente. Ainsi, on comprend la nécessité d’imposer un système d’unités de référence (mètre, pouce, kilogramme,…), le même pour tous, car tout le monde ne possède pas une règle graduée en capuchon de stylo. Avoir un ensemble d’unités commune permet de communiquer ses mesures beaucoup plus facilement.
- Pour certaines grandeurs, il peut être nécéssaire d’utiliser une unité dérivée, c’est-à-dire une combinaison de plusieurs unités. C’est le cas par exemple de la vitesse qui représente une distance pendant un temps : [math]\displaystyle{ vitesse = \frac{longueur}{temps} }[/math] .
- Comme expliqué plus haut, une même grandeur peut être exprimée selon des unités différentes, toutes convenables. Une longueur peut donc être exprimée en mètre, kilomètre, mile (unité de mesure dans le système anglo-saxon)…. De la même façon, un temps peut être exprimé en seconde, minute, heure, etc.
- De cette façon, les unités dérivées peuvent être très variées pour une seule grandeur. La vitesse peut donc s’exprimer en kilomètre par heure (km/h) ou en mètre par seconde (m/s) ou bien encore en centimètre par minute (cm/min) et on peut passer d’une unité à l’autre en multipliant par le nombre qui convient. Tout ce qui compte c’est que la dimension, c’est-à-dire la combinaison des grandeurs, reste la même, pour la vitesse on doit toujours avoir : [math]\displaystyle{ vitesse = \frac{longueur}{temps} }[/math] .
- Note
- Passage d’une unité à l’autre.
Pour que les unités d’une même grandeur soit cohérentes, elles doivent toutes être reliées par une multiplication. Par exemple 1 heure = 60 x 1 minute = 60 x 60 x 1 seconde, ou encore 1 kilomètre = 1 000 x 1 mètre.
Pour récapituler :
| Grandeur | On appelle grandeur physique, ou simplement grandeur, toute propriété de la science de la nature qui peut être mesurée ou calculée (ex : la longueur, la masse, la température, …) |
| Unité | On appelle unité de mesure un cas particulier de la grandeur considérée qui sert de référence pour la mesure (ex : le centimètre, le kilogramme,…) et est déduite à partir d’un étalon fixée. |
| Unité dérivée | On appelle unité dérivée une unité qui s'écrit comme la combinaison (multiplication et division) d'unités de base |
| valeur | La valeur mesurée d’une grandeur est le produit (multiplication) de l’unité de mesure par le nombre de fois qu’il faut reporter cette unité pour obtenir la grandeur (ex : 3cm, 1,5 kg,…) |
Vous avez remarqué que la mesure du bâton avec le stylo paraissait moins certaine que celle avec les capuchons ? Allez donc consultez la page sur les incertitudes pour en apprendre plus sur cette notion.
Les constantes fondamentales
En physique, il existe des quantités fixes et universelles qui font partie de la description du monde que l’on observe. Ces quantités peuvent être naturelles, et interviennent dans des équations de la physique, ou être techniques, et correspondent dans ce cas à un choix technique. Qu’elles soient naturelles ou techniques, ces quantités sont regroupées sous le même nom de constante fondamentale (ou encore constante universelle).
La plus connue est probablement la vitesse de la lumière, notée c, mais en réalité on en connaît 7.
| Constante | Symbole | Valeur numérique | Unité |
| Fréquence de la transition hyperfine du Césium | [math]\displaystyle{ \Delta \nu_{Cs} }[/math] | [math]\displaystyle{ 9~ 192 ~631~ 770 }[/math] | Hz |
| Vitesse de la lumière dans le vide | [math]\displaystyle{ c }[/math] | [math]\displaystyle{ 299 ~792 ~458 }[/math] | [math]\displaystyle{ m.s^{-1} }[/math] |
| Constante de Planck | [math]\displaystyle{ h }[/math] | [math]\displaystyle{ 6,626 ~ 070 ~15 \times 10^{-34} }[/math] | J s |
| Charge élémentaire | [math]\displaystyle{ e }[/math] | [math]\displaystyle{ 1,602 ~176 ~634 \times 10^{-19} }[/math] | C |
| Constante de Boltzmann | [math]\displaystyle{ k }[/math] | [math]\displaystyle{ 1, 380 ~649 \times 10^{-23} }[/math] | [math]\displaystyle{ J ~K^{-1} }[/math] |
| Constante d'Avogadro | [math]\displaystyle{ N_A }[/math] | [math]\displaystyle{ 6,022 ~140 ~76 \times 10^{23} }[/math] | [math]\displaystyle{ mol^{-1} }[/math] |
| Efficacité lumineuse | [math]\displaystyle{ K_{cd} }[/math] | 683 | [math]\displaystyle{ lm W^{-1} }[/math] |
Le système international d’unités
Comme expliqué dans la partie concernant les notions de grandeur et d’unité, une même grandeur peut être exprimée selon différentes unités, a priori toutes valables. Afin de faciliter la mesure et la communication d’un pays à l’autre ou d’une personne à l’autre, la plupart des pays ont choisi de s’accorder sur des unités officielles. Cet ensembles d’unités officielles est appelé Système International d’Unités (l’abréviation est « SI »)et a été officiellement défini en 1960.
Les unités de ce système sont décidées par 3 organismes internationaux : La Conférence générale des poids et mesures (CGPM), le Comité international des poids et mesures (CIPM) et le Bureau international des poids et mesures (BIPM) tous créés lors de la Convention du Mètre en 1875 .

Ces unités sont au nombre de 7 :
| Unité du SI | Symbole | Grandeur qu'elle représente |
| Le mètre | m | longueur |
| Le kilogramme | kg | La masse |
| La seconde | s | Le temps |
| L'ampère | A | L'intensité du courant électrique |
| Le kelvin | K | La température |
| Le candela | cd | L'intensité lumineuse |
| La mole | mol | La quantité de matière |
Pourquoi exprimer les unités du système international en fonction des constantes fondamentales ?
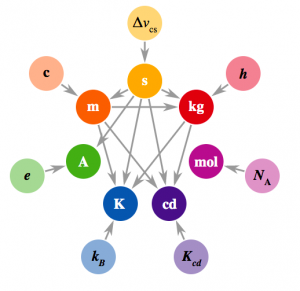
Depuis les débuts de la métrologie (science qui étudie la mesure et les unités), les unités de base qui constituent le SI ont souvent changé de définition. Effectivement, on peut établir la définition d'une unité de 3 manières différentes : Ou bien l'unité est définie par un étalon physique matériel (un prototype dont la valeur vaut l'unité), ou bien l'unité est défini à partir d'une caractéristique physique (le mètre a d'abord été défini comme la 10 000 000e partie d'une moitié de méridien terrestre), ou bien on peut définir une unité de façon immatérielle, à l'aide d'une relation impliquant des constantes fondamentales de la nature.
Le kilogramme fût défini selon un prototype matériel que l'on conservait en lieu sur, et le kelvin fût défini un temps comme la température à laquelle l'eau forme des glaçons et se met à bouillir ([le point triple]). Ces définitions posent problème , car on a remarqué que les prototypes matériels (comme cela était le cas pour le kilogramme) changeait de valeur au cours du temps (à cause de procédés chimiques internes) , et certaines définitions exigeaient des réalisations pratiques idéales, qui en fait étaient impossible en pratique. De plus, le CIPM (organisme qui fixe le SI) souhaitait établir un système dans lequel les mesures des unités sont liées entre elles, ce qui le rendrait plus cohérent.
Ainsi, depuis 2018 l'ensemble des 7 unités de base sont définies à partir des constantes fondamentales de la physique, qui sont intemporelles , théoriques, et mettent en jeu des unités dérivées (ce qui permet de lier les définitions des unités de base).
Par exemple pour la nouvelle définition du kilogramme, on part de la constante de Planck ([math]\displaystyle{ h }[/math]) :
[math]\displaystyle{ h = 6,626 ~ 070 ~15 \times 10^{-34} J.s = 6,626 ~ 070 ~15 \times 10^{-34} m^2kg/s }[/math] où l'on a remplacé l'unité dérivée J (le joule) par la combinaison d'unité de base qui lui correspond ([math]\displaystyle{ 1 J = 1~ kg ~ m^2 ~ s^{-2} }[/math] )
Ensuite on retourne cette équation pour isoler l'unité de base qui nous intéresse et l'exprimer en fonction de la constante fondamentale concernée :
[math]\displaystyle{ 1 ~kg = (\frac{h}{6,626 ~ 070 ~15 \times 10^{-34}})\times m^{-2} \times s }[/math] où le mètre et la seconde sont définis indépendamment. ( la notation [math]\displaystyle{ m^{-2} }[/math] signifie que l'on divise 2 fois par [math]\displaystyle{ m }[/math] ).
C'est de cette façon que les unités de base du SI sont actuellement définies.
Bibliographie/Webographie
- Site du réseau national de la métrologie française [consulté en juin 2021] : https://metrologie-francaise.lne.fr/fr/metrologie/unites-de-mesure-si
- Site du Bureau National des Poids et Mesures (BIPM) [consulté en juin 2021] : https://www.bipm.org/fr/measurement-units/si-defining-constants
- Article de Futura Science sur le point triple [consulté en juin 2021] : https://www.futura-sciences.com/sciences/definitions/physique-point-triple-15345/