Incertitudes de mesure
Toute mesure est réalisée avec une incertitude. Cette incertitude peut être due à l'erreur humaine, à la précision limitée de l'appareil de mesure... Ainsi, lorsqu'on présente un résultat de mesure, il est important de préciser l'incertitude correspondante afin de pouvoir évaluer la précision de ce résultat.
On présente généralement un résultat sous la forme: [math]\displaystyle{ M=m\pm \Delta M }[/math] avec [math]\displaystyle{ M }[/math] le résultat final de la grandeur mesurée, [math]\displaystyle{ m }[/math] la valeur estimée du résultat de cette grandeur (lue sur l'appareil de mesure) et [math]\displaystyle{ \Delta M }[/math] l'incertitude associée. Cela signifie que le résultat de la mesure est compris dans l'intervalle [math]\displaystyle{ [m+\Delta M, m-\Delta M] }[/math].
Prenons un exemple concret:
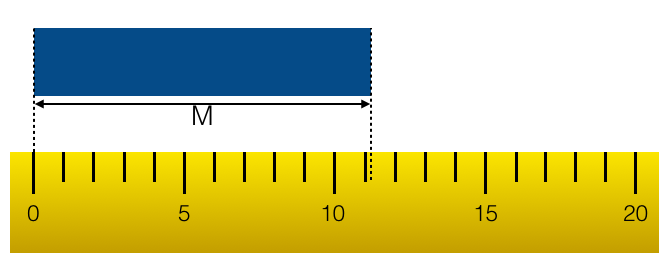
On cherche ici à mesurer la longueur de l'objet bleu. Pour cela, on utilise une règle graduée toutes les centimètres. On trouve que la longueur est légèrement au dessus de 11cm, mais les graduations ne nous permettent pas de déterminer précisément à quel endroit entre 11 et 12cm la longueur se situe. On peut alors écrire que [math]\displaystyle{ M = 11\pm 1 cm }[/math]. Cela veut dire que la longueur de l'objet est comprise entre [math]\displaystyle{ 10cm }[/math] et [math]\displaystyle{ 12cm }[/math].
Comment réduire les incertitudes?
Pour réduire les incertitudes sur une mesure, et donc effectuer une mesure plus précise, on peut tout d'abord utiliser un instrument de mesure plus précis. Par exemple, dans le cas de notre règle graduée, une règle graduée tous les millimètres aurait permis de déterminer la longueur de l'objet au millimètre près.
Une autre technique peut être de répéter la même mesure dans des conditions strictement identiques, et d'effectuer une moyenne de tous les résultats de mesure obtenus. En effet, la moyenne de plusieurs mesures est plus proche de la valeur vraie que la valeur d'une seule mesure.
Fidélité et justesse

Imaginons que nous répétons plusieurs fois la même mesure, avec le même instrument, dans des conditions identiques, et traçons une croix sur un cercle pour chacun des résultats obtenus. On suppose que la valeur vraie de la mesure se situe au centre du cercle.
Un instrument est dit fidèle si on observe peu de dispersion. Les points sont centrés autour de leur moyenne, mais pas autour de la valeur vraie. On parle alors d'erreur systématique.
Il est dit juste si les points sont situés autour de la valeur vraie, mais très dispersés. Il y a alors peu d'erreur systématique, mais l'instrument n'est pas précis.
Enfin, si l'instrument est fidèle et juste, on dit qu'il est exact. Les points sont centrés autour de la valeur vraie.
Notation scientifique
La notation scientifique est utilisée par les scientifiques lorsqu'ils doivent écrire de très grands ou de très petits nombres.
Elle consiste à écrire les nombres sous la forme: [math]\displaystyle{ a\times 10^{n} }[/math] avec [math]\displaystyle{ 1\leq a\lt 10 }[/math] et [math]\displaystyle{ n }[/math] un nombre entier.
Un exemple: pour faciliter les calculs, on arrondi souvent la vitesse de la lumière à 300 000km/s, soit 300 000 000m/s. En notation scientifique, ce nombre s'écrit: [math]\displaystyle{ 3\times 10^{8} }[/math]m/s.
Chiffres significatifs
Il est important, lorsqu'on publie un résultat, d'exprimer l'incertitude correspondante, avec le bon nombre de chiffres significatifs, c'est à dire des chiffres qui ont une signification réelle.
Pour connaitre le nombre de chiffres significatifs d'un nombre, il faut suivre quelques règles:
- Les chiffres non nuls (différents de 0) sont toujours significatifs
- Un 0 n'est pas significatif s'il est placé en tête du nombre
- Un 0 est significatif s'il est placé à la fin du nombre.
Quelques exemples:
- 42 : 2 chiffres significatifs
- 4,2 : 2 chiffres significatifs
- 0,42 : 2 chiffres significatifs
- 0,420 : 3 chiffres significatifs
Si on reprend l'exemple de notre règle graduée tous les centimètres, dire que m vaut 11,2cm n'a pas de sens, puisque la règle n'est pas assez précise.
Lorsque l'on additionne, soustrait, divise ou multiplie des nombres, le résultat ne doit pas avoir plus de décimales que le nombre qui en a le moins.
Exemple: calculons par exemple le périmètre [math]\displaystyle{ p }[/math] d'un cercle de rayon [math]\displaystyle{ r=4,2cm }[/math]. On utilise la formule: [math]\displaystyle{ p=2\pi r }[/math]. La calculatrice nous donne alors [math]\displaystyle{ p=26,389378902... }[/math] Mais [math]\displaystyle{ r }[/math] n'ayant que deux chiffres significatifs, il faut écrire [math]\displaystyle{ p=26cm }[/math]. Pour écrire ce résultat en unités du Système International, il faut écrire : [math]\displaystyle{ p=2,6\times 10^{-1}m }[/math].
Pour arrondir un nombre avec le bon nombre de chiffres significatifs, on utilise la règle suivante:
- Si le chiffre suivant est 0, 1, 2, 3 ou 4: on arrondi à l'inférieur
- Si le chiffre suivant est 5, 6, 7, 8 ou 9: on arrondi au supérieur.
Exemple: on veut arrondir au dixième (un chiffre après la virgule) les nombres suivants:
- 1,456 devient 1,5
- 1,042 devient 1,0
Bibliographie/Webographie
LANGEVIN-JOLIOT, Hélène ; HAÏSSINSKI, Jacques. Science et culture : Repères pour une culture scientifique commune. Éd. Apogée, 2015, 160 p. ISBN 978-2-84398-473-0
Eduscol : Mesure et incertitudes. [en ligne]. Ressources pour le cycle terminal général et technologique. © MENJVA/DGESCO-IGEN. [consulté le 6 juillet 2016]. Disponible sur internet: <http://national.udppc.asso.fr/attachments/article/537/_ressources_MathPC_Mesure_et_incertitudes_eduscol_214070.pdf>