Distances dans l'univers
|
|
Méthodes antiques
Dès l'antiquité les grecs avaient trouvé des méthodes pour effectuer certaines mesures. Ainsi Eratosthène avait réussi a faire une assez bonne mesure du rayon de la Terre. Aristarque de Samos, lui, s'est penché sur la mesure du rayon de la Lune et de la distance entre la Terre et la Lune.Pour la mesure du rayon de la Lune, l'idée de départ est de supposer que le premier et le dernier quartier de la Lune sont alignés (c'est à dire que la durée entre le dernier quartier et la nouvelle Lune est le même que la durée entre la nouvelle Lune et le premier quartier).
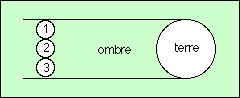
A partir de là, il suffit de remarquer qu'une éclipse totale de Lune dure environ deux heures. De plus la Lune se déplace dans le ciel de son propre diamètre en 1h. La Lune est donc environ trois fois plus petite que la Terre. Si on note [math]\displaystyle{ L }[/math] le diamètre de la Lune et [math]\displaystyle{ T }[/math] celui de la Terre, on a [math]\displaystyle{ L = 0.3 T }[/math]. Connaissant le diamètre terrestre (grâce à Ératosthène), on peut connaître le rayon de la Lune.
Ensuite, pour déterminer la distance Terre-Lune, on détermine sous quel angle on vois la Lune depuis la Terre. Cet angle est de 32' d'arc environ.
|
|
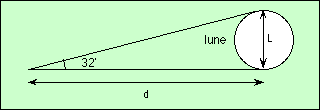
On a donc [math]\displaystyle{ d = \frac{0.3T}{0.0093} = 32T = 64R }[/math] ou [math]\displaystyle{ R }[/math] désigne le rayon de la Terre.
Aujourd'hui on mesure cette distance à environ 60R, le résultat obtenu par Aristarque est donc d'une précision excellente pour l'époque.
Des méthodes similaire peuvent être utilisées pour mesurer la distance entre la Terre et le Soleil ou encore d'autres distances dans le système solaire. Il faut noter que ces méthodes, si elles peuvent donner des ordres de grandeurs pertinents, donnent des résultats peu précis. De plus ce sont des méthodes qui donnent toujours des longueurs relatives (comme pour la Lune ou les distances étaient calculés comme des multiples du rayon terrestre), ce qui limite la précision des mesures à celle des mesures précédentes.
Méthode de la parallaxe
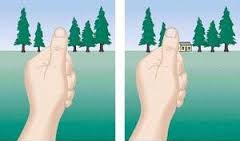
Pour comprendre en quoi cela consiste une expérience simple peut être réalisée. Si on tend le bras, pouce levé, devant ses yeux, que l'on ferme un œil et que l'on cache un objet éloigné avec son pouce puis que l'on inverse l’œil fermé et l’œil ouvert, on vois que le pouce ne cache plus l'objet.
Ce phénomène est un effet de perspective (que l'on nomme parallaxe, d'où le nom de la méthode) dû à la distance entre les yeux. Cet effet est d'autant plus marqué que l'objet observé est proche, ou, plus exactement, que le rapport [math]\displaystyle{ \frac{d}{e} }[/math] est petit ([math]\displaystyle{ e }[/math] désigne l'écart entre les yeux et [math]\displaystyle{ d }[/math] la distance entre l'observateur et l'objet). Avec la connaissance de l'écart entre les deux et de l'angle sous lequel on vois l'objet, on peut remonter à la distance entre l'observateur et l'objet. Notre fait des calculs de ce genre en permanence. C'est ce qui nous permet d'avoir une vision 3D.
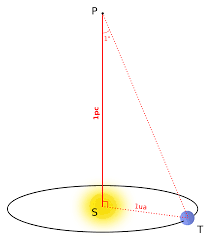
Ils ont pris une première photo d'un coté de l'orbite terrestre et une seconde photo six mois plus tard, de l'autre coté de l'orbite terrestre.
|
|
Aujourd'hui de nombreuses mesures ont été faites dans l'espace par des satellites. Ainsi le satellite Hipparcos (HIgh Precision PARallax COllecting Satellite), lancé le 8 août 1989, a produit trois catalogues :
Le catalogue Hipparcos contient 120 000 étoiles situées à moins de 500 AL (Année Lumière) avec une très bonne précision (de l'ordre du millième de seconde d'arc).
Le catalogue Tycho contient plus d'un million d'étoiles, avec une précision de 20 à 30 mas (micro seconde d'arc).
Le catalogue Tycho 2 est une extension du précédent. Il contient 2.5 millions d'étoiles avec une précision légèrement améliorée. Il contient 99% des étoiles de magnitude inférieur à 11.
|
|
Le satellite Gaïa : Lancé en décembre 2013 pour une mission de cinq ans, il est cinquante fois plus précis qu'Hipparcos. Il va observer plus d'un milliard d'étoiles jusqu'à magnitude 20 (position, photométrie, spectrométrie). Cela représente environ 1% des étoiles de la Voie Lactée. Il va déterminer les positions avec une précision de 300 microseconde d'arc (0.3 millième de seconde d'arc) soit 10 000 fois plus d'étoiles que le satellite Hipparcos, avec trois fois plus de précisions. Il sera également capable d'observer des étoiles plus lointaines que Hipparcos : une étoile similaire au soleil ([math]\displaystyle{ M = 5 }[/math]) est vue à [math]\displaystyle{ m = 12 }[/math] à 250pc et à [math]\displaystyle{ m = 20 }[/math] à 10 000pc, soit 40 fois plus loin !
Jusqu'à cette distance (30 000 AL) la précision est meilleure que 20%.
Pour les étoiles plus proche ( [math]\displaystyle{ m = 12 }[/math] ) la précision est meilleur que 7 micro seconde d'arc (7 millionième de seconde d'arc). Cela reviens à voir depuis la Terre une pièce de 1 euros posée sur la surface de la Lune.
Mesure par Laser
Pour des "courtes" distances (Typiquement, Terre-Lune) on peut mesurer la distance grâce à un laser. On dépose un réflecteur laser sur la Lune (par exemple) puis on pointe un laser sur le réflecteur et on mesure le temps que prend le laser pour faire l'aller retour. C'est une mesure d'une très grande précision mais elle est compliquée à utiliser car il faut avoir posé un réflecteur sur l'objet et être suffisamment proche pour viser précisément le réflecteur.
Grâce à cette méthode on a pu mesurer, notamment, que la Lune s'éloigne de la Terre de 3.8cm/an.
Il existe une méthode similaire pour les objets plus éloignés en utilisant des ondes radar à la place du laser. Ainsi il n'y a plus besoin de réflecteur. Cette méthode reste limitée car la réflexion des ondes radar est faible. On arrive toutefois à mesurer des distances telles que la distance Terre-Venus avec une précision meilleur que le kilomètre.
Méthodes Physiques
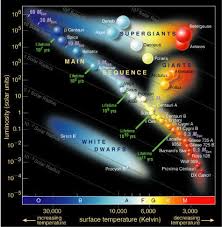
Diagramme de Hertzsprung-Russell
Ce diagramme est très utilisé par les astrophysiciens. Il représente la luminosité (magnitude absolue) des étoiles en fonction de leur température. Un élément remarquable de ce diagramme est la séquence principale : Une grande partie des étoiles semblent se répartir sur une droite approximative. L'idée est alors, pour un groupe d'étoiles rapprochées (que l'on appelle amas), de tracer ce diagramme en fonction de la magnitude apparente plutôt qu'en fonction de la magnitude absolue. Il y a dans l'amas de nombreuses étoiles différentes qui vont donc être répartie sur la séquence principale. Ainsi, si l'on trace le diagramme en fonction de la magnitude apparente, on va observer un décalage vertical par rapport au diagramme classique. En mesurant ce décalage, on peut alors remonter à la distance entre l'observateur et l'amas.
Les Céphéides
Cette méthode date du début du XXème siècle. Elle se base sur l'existence d'étoiles dites variables. Ce sont des étoiles dont la luminosité varie. Parmi ces étoiles, une catégorie particulière, appelée 'Céphéides varient de manière très régulière. De plus l'astronome Henrietta Leavitt a montré que la période de variation de la luminosité de ces étoiles est liée à leur magnitude absolue. On peut déterminer la relation exacte grâce à des étoiles proches.
Les céphéides sont des étoiles très brillantes, on peut donc les observer, même à de grandes distances et permettent donc de mesurer la distance d'amas (et même de galaxies) qui les contiennent. Toutefois, à partir d'une certaine distance, ces étoiles ne sont plus suffisamment lumineuses. Il faut alors utiliser d'autres méthodes basées sur des objets plus lumineux.
Loi de Tully-Fisher
En 1977 deux astronomes anglais, Tully et Fisher, découvrent une relation (empirique) entre la vitesse de rotation d'une galaxie spirale et sa luminosité. On peut calibrer la relation (déterminer la valeur des constantes) sur des galaxies proches.
On se base d'abord sur un effet que l'on appelle Doppler-Fizeau pour calculer la vitesse de rotation de la galaxie, puis il suffit d'utiliser la loi de Tully-Fisher pour obtenir la magnitude absolue. On compare celle-ci à la magnitude absolue que l'on observe et on remonte ainsi à la distance entre l'observateur et la galaxie.
Cette méthode est toutefois peu précise. De plus elle ne marche que pour certaine galaxies que l'on appelle galaxies spirales.
Loi de Faber-Jackson
C'est une loi similaire à la loi de Tully-Fisher mais qui s'applique, cette fois, aux galaxies elliptiques. Le principe globale est le même, en remplaçant la vitesse de rotation par la dispersion de vitesse.
Méthodes Cosmologiques
Il existe encore d'autre méthodes qui se basent sur les découvertes du siècle dernier en cosmologie et en relativité générale. Elle sont toutefois plus complexes à mettre en place, ne marchent que pour des objets très très éloignés et sont assez peut précises.
Bibliographie/Webographie
Mesure des distances [en ligne, consulté le 16 juin 2017]. Disponible sur internet : <https://astronomia.fr/1ere_partie/distances.php>
Comment mesure-t'on aujourd'hui la distance des étoiles ? [en ligne, consulté le 16 juin 2017]. Disponible sur internet : <http://www.astrosurf.com/toussaint/dossiers/distances/distances2.htm>
La détermination des distances en astronomie [en ligne, consulté le 16 juin 2017]. Disponible sur internet : <http://www.ago.ulg.ac.be/PeM/Docs/distanceYN.pdf>
L’Univers et sa mesure [en ligne, consulté le 16 juin 2017]. Disponible sur internet : <http://lal.univ-lille1.fr/docpedago/CoursAstro1LSTAS1.pdf>
Mesures de distances dans l'Univers [en ligne, consulté le 16 juin 2017]. Disponible sur internet : <http://www.astrosurf.com/quasar95/exposes/distances_dans_l'univers.pdf>

